Embedded Files
Objectives Covered:
NC.4.NF.3: Understand and justify decompositions of fractions with denominators of 2, 3, 4, 5, 6, 8, 10, 12, and 100.
• Understand addition and subtraction of fractions as joining and separating parts referring to the same whole.
• Decompose a fraction into a sum of unit fractions and a sum of fractions with the same denominator in more than one way using area models, length models, and equations.
• Add and subtract fractions, including mixed numbers with like denominators, by replacing each mixed number with an equivalent fraction, and/or by using properties of operations and the relationship between addition and subtraction.
• Solve word problems involving addition and subtraction of fractions, including mixed numbers by writing equations from a visual representation of the problem
NC.4.NF.4: Apply and extend previous understandings of multiplication to:
• Model and explain how fractions can be represented by multiplying a whole number by a unit fraction, using this understanding to multiply a whole number by any fraction less than one.
• Solve word problems involving multiplication of a fraction by a whole number
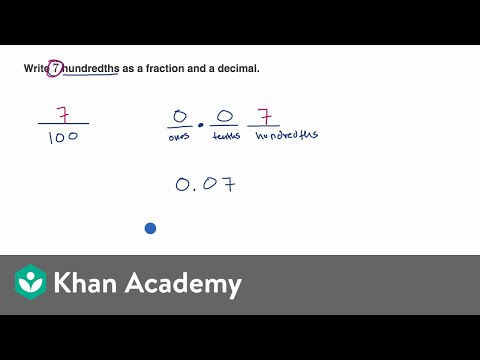
NC.4.NF.6: Use decimal notation to represent fractions.
• Express, model and explain the equivalence between fractions with denominators of 10 and 100.
• Use equivalent fractions to add two fractions with denominators of 10 or 100.
• Represent tenths and hundredths with models, making connections between fractions and decimals
NC.4.NF.7: Compare two decimals to hundredths by reasoning about their size using area and length models, and recording the results of comparisons with the symbols >, =, or <. Recognize that comparisons are valid only when the two decimals refer to the same whole.
Essential Question
Essential Question
4.NF.3: How do you add and subtract fractions and mixed numbers with common denominators
4.NF.3: How do you add and subtract fractions and mixed numbers with common denominators
4.NF.4: How do you multiply fractions by whole numbers?
4.NF.4: How do you multiply fractions by whole numbers?
4.NF.6: How would you read, model and convert decimals to the hundredths?
4.NF.6: How would you read, model and convert decimals to the hundredths?
4.NF.7: How can you use strategies to compare tenths to hundredths (fractions and decimals)
4.NF.7: How can you use strategies to compare tenths to hundredths (fractions and decimals)
Vocabulary
Vocabulary
-denominator -equivalent fractions
-denominator -equivalent fractions
-fraction -model
-fraction -model
-numerator -compare
-numerator -compare
-common denominator-mixed numbers
-common denominator-mixed numbers
-improper fractions -decimals
-improper fractions -decimals
-tenths -hundredths
-tenths -hundredths
-decimal point
-decimal point
Converting Mixed Numbers to Improper Fractions:
Converting Mixed Numbers to Improper Fractions:
In our class we use three methods to convert mixed numbers into improper fractions:
Modeling (can be either a model or a number line)
Addition of whole fractions and partial fractions
MAN Strategy
Multiply denominator & whole number
Add
Numerator
Converting Mixed Improper Fractions to Mixed Numbers:
Converting Mixed Improper Fractions to Mixed Numbers:
In our class we use three methods to convert improper fractions:
Modeling (build UP to get to the improper fractions)
Subtract whole fractions; *Can I take away another whole? Keep going until you can't!
DND Strategy
Divide
Numerator from
Denominator
Whole Number = Quotient
Numerator = Remainder
Denominator stays the same
Adding Mixed Numbers:
Adding Mixed Numbers:
1. Add the wholes
2. Add the fractions
*3. IF you end up with an improper fraction, change it to a mixed number
*4. THEN combine the mixed number with the ORIGINAL whole number to get your sum
Subtracting Mixed Numbers:
Subtracting Mixed Numbers:
Strategy 1: Models
Draw/shade first number
Cross out 2nd fractional amount, then whole
Count up how much isn't shaded
Strategy 2: Change to Improper Fractions
Change mixed numbers into Improper fractions
Subtract
Change answer back into mixed number
Strategy 3: "Regroup" from whole
Regroup a "whole" into a fraction; so whole number goes down, fraction increases by a fractional whole
ex. 4 and 2/3; 4 would go to 3 then the "whole" would be 3/3 so the fraction would now be 5/3 (3/3+2/3)
Multiplying Whole Numbers and Fractions
Multiplying Whole Numbers and Fractions
-Strategy 1: Models
-Strategy 2: Number Lines
-Strategy 3: Repeated Addition
-Strategy 4: Multiply numerator and whole number
*watch out for improper fractions; may need to be changed to mixed numbers
**correction to anchor chart below; in the Multiply Whole # by Numerator strategy my note says "numerator stays the same" and SHOULD say "denominator stays the same"**
Decimals
Decimals
Always try to connect decimals to fractions
Remember 1/10 and 0.1 are equivalent and 1/100 and 0.01 are equivalent.
"Read the place value" to connect to decimals to fractions
Decimals can be expressed as fractions, on a grid, in words or on a number line
If there are hundredths but no tenths, make sure there is a "0" as a place holder in the tenths place
Report abuse